やり方 分数 の 足し算 195610

仮分数 帯分数 真分数とは 帯分数の掛け算などの応用問題４選も解説 遊ぶ数学

 分母が小さい方を大きい方に合わせてあげましょう。 1 5 = 1 × 2 5 × 2 = 2 10 となります。 解答2 1 5 2 10 = 2 10 2 10 = 4 10 = 2 5 よって答えは 2 5 です。 もう少し詳しい分数の足し算は別記事を用意しました。 帯分数がある場合の足し算や、分母はそのままで良い理由を解説しています。 分数の足し算やり方を問題で解説｜約分・通分も工学博士監修分数の足し算は、通分によって分母をそろえてから分子を足す ことで計算できます。 計算の手順は次の 3 ステップになります。 分数の足し算のやり方 通分（分母をそろえる） 分子同士を足す 約分する 例えば、次のように足し算を計算できます。 1 2 1 3 = 3 6 2 6 = 3 2 6 = 5 6 1 2 1 3 = 3 6 2 6 = 3 2 6 = 5 6 このページでは、 分母が同じ分数の足し算のやり方 と

やり方 分数 の 足し算

やり方 分数 の 足し算-2 分配法則を使う平方根の掛け算・割り算 21 乗法公式を使って式の展開をする 分数の足し算 分数の足し算は ①：2つの分数の「分母」が同じになるようにそろえて(通分して)から ②：2つの分数の「分子」を足し算をして ③：最後に「約分」をする。 この 3つのステップをふむのがコツ です。 ここでは、「2/3 1/12」を計算してみましょう。

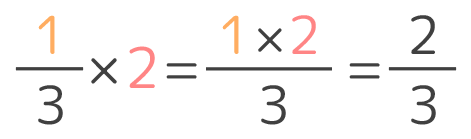
小学5年生 帯 真 分数と整数のかけ算 を図解 そうちゃ式 分かりやすい図解算数 別館

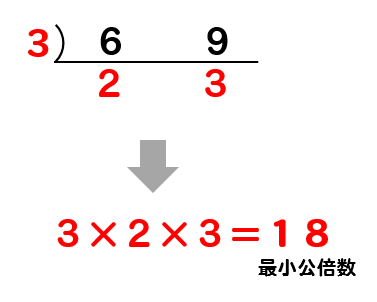
 分数の通分"チョウ分数"｜分子が1の場合 通分"チョウ分数"足し算（加法） チョウ分数の解き方の手順 ①分母と分母の間に、チョウのしっぽをかく。 ②ななめにちょうの羽根をかき、分子のほうに触角をかく。 ③羽根の中に入っている分母と分子をかける。 ④残りも、同じように羽根をかいて、分母と分子をかける。 ⑤数字のないチョウを描いて 分数の足し算のまとめ 小学3年生の分数の教え方についてお話ししてきました。 日常生活で使われる計算方法ですので、物に例え説明するとわかりやすいでしょう。 『もとの数を1としたときの、何分の何？ 』 を理解しておくことが重要です。 今は、1やり方や最小公倍数を簡単に計算するコツも解説 学び通信 分数の勉強をして急激に難しいなと感じるところが通分です。 通分は分母の違った分数同士を足し算・引き算をする際に分母をそろえるのですが、その時に最小公倍数の仕方が分かればあっという間に通分ができますので確認していきましょう。 スマイルゼミ スマイルゼミのキャンペーンコードは

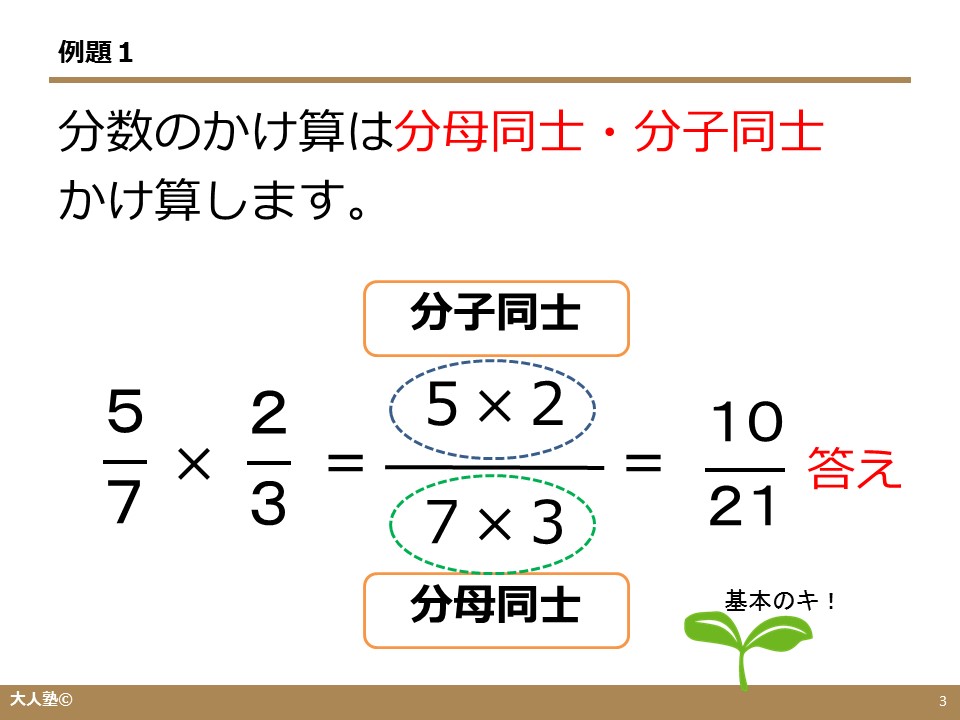
 分数の足し算・引き算・掛け算・割り算のやり方 を一覧にまとめました。 それぞれの計算の仕方を忘れてしまった場合は、こちらで確認しましょう。 （基本的な問題もあわせて練習できるようになっています。 ） 分数の足し算やり方と問題 分数の引き算やり方と問題 分数の掛け算やり方と問題 分数の割り算やり方と問題 分数の計算 分数はそれまで学習してきた数と異なり、独特の表記をします。 例えば では、分母である「3」は基準となる 「1」の分割量 、 分子である「2」は「1/3」の 数量 を表しているのですが、 今までの学習では、全て数字を「数量」として認識してきたためそして、わり算を分数の形で表したモノが\(\displaystyle \frac{3}{10}\)というわけです。 なんで\(\displaystyle \frac{3}{10}\)になるのか？？ 分数の割り算を思い出してみましょう。 $$\Large{3\div 10=3\div \frac{10}{1}}$$ $$\Large{=3\times \frac{1}{10}}$$ $$\Large{=\frac{3}{10}}$$

やり方 分数 の 足し算のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	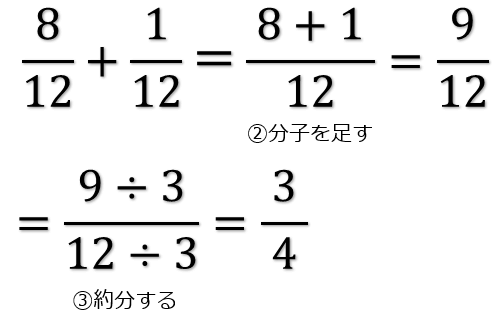簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	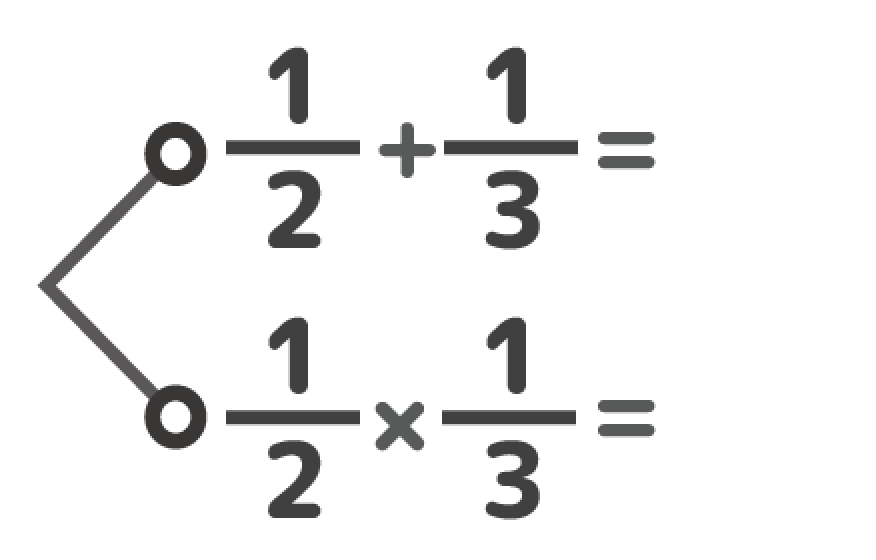簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	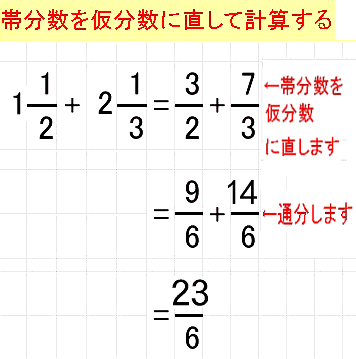簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	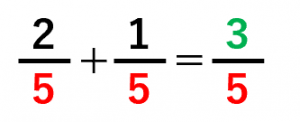簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	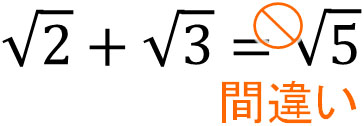簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	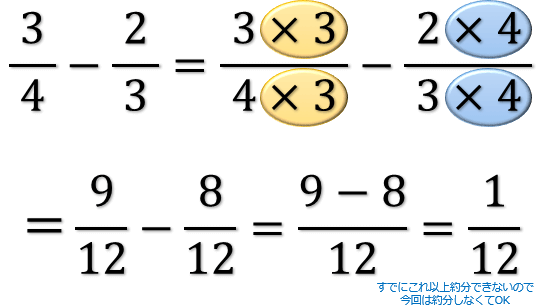簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	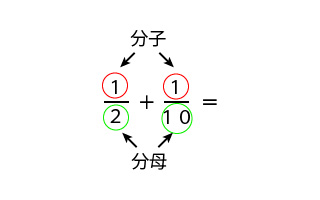簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	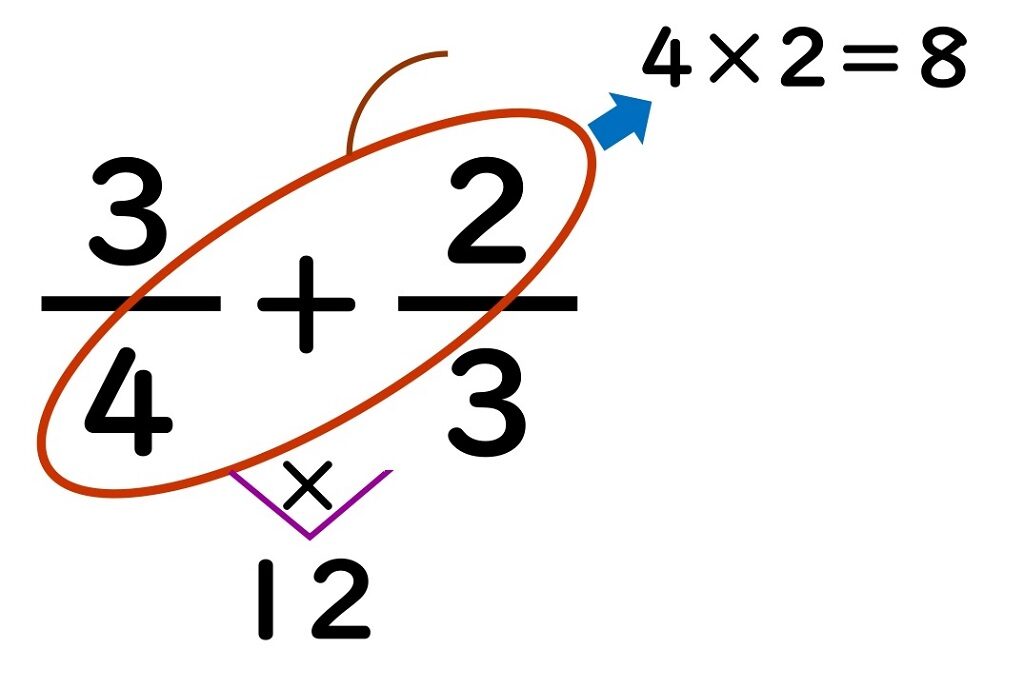簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
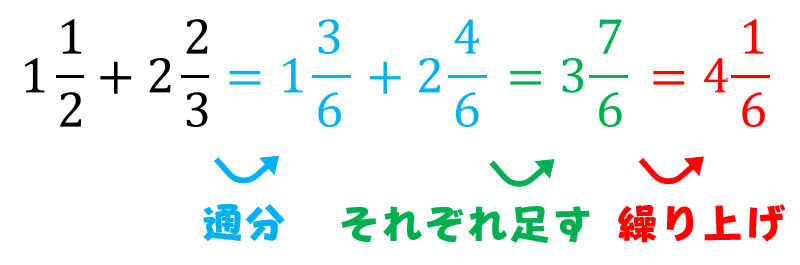簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
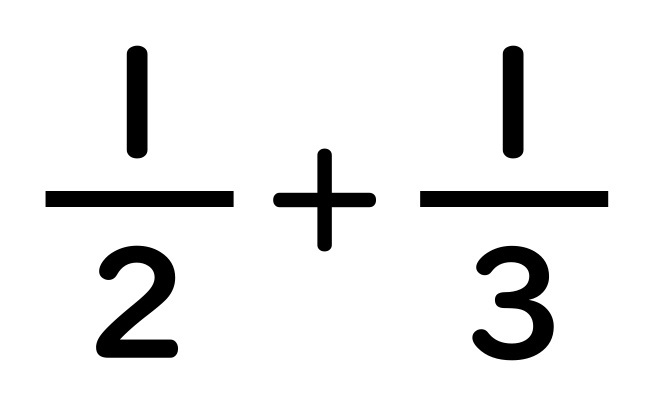簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
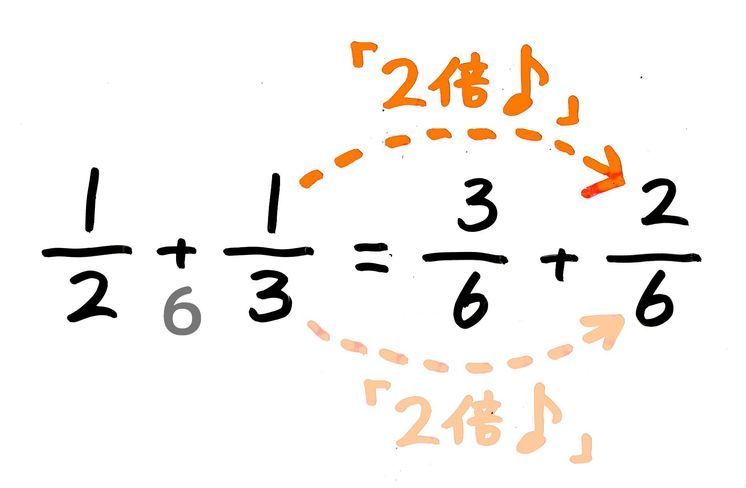簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
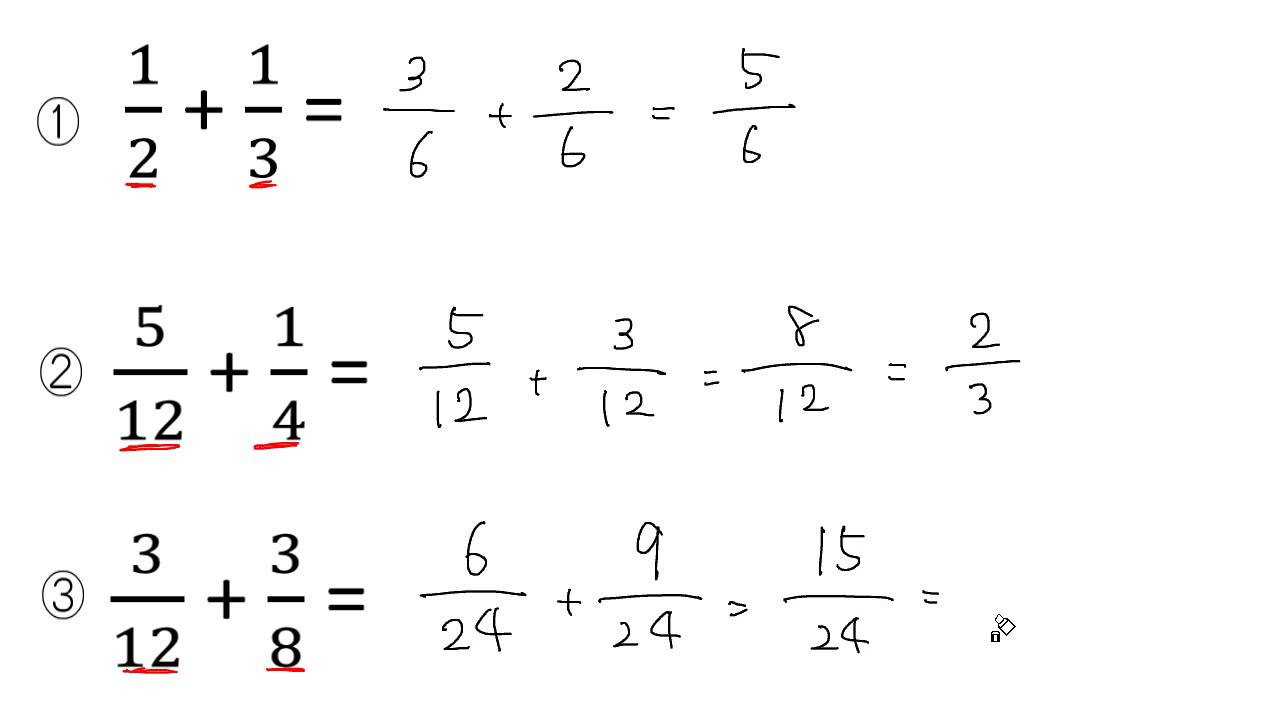簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	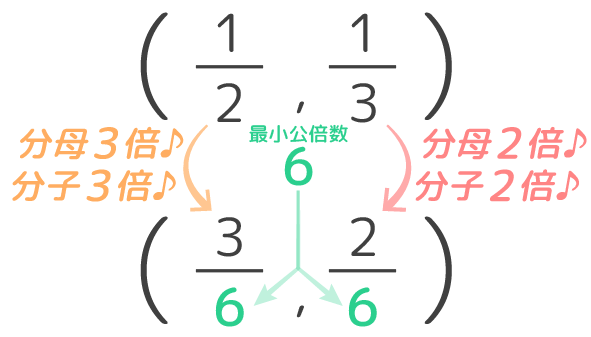簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
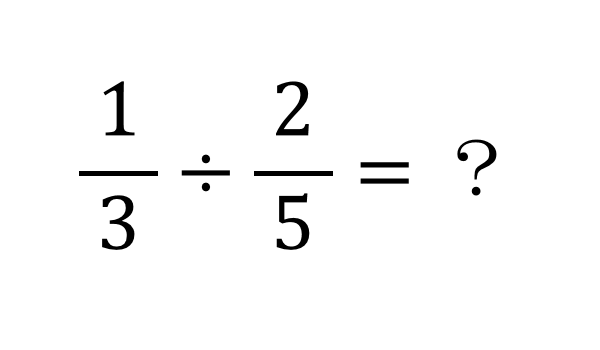簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説	簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説

 部分分数分解とは「分数のかけ算を分数の足し算（引き算）に変形すること」を指します。 例えば、 1 = 1 4 × 5 は 1 4 × 5 = 1 4 − 1 5 と変形できますよね。 この操作のことを「 1 4 × 5 を部分分数分解する」と言います。 微分 や 積分 など、複雑な計算をするときは 部分分数分解で「分数の足し算」に変形すると計算が楽になる ケースが少なくありません。 部分分数分解をマスターす方法 1仮分数を足す 分母の最小公倍数を見つける 足し算をする前に分母をそろえる必要があるので、まず2つの分母の数字の公倍数を見つけましょう。 そして、その中から最も小さな数字を選びましょう。 例えば、 9/5 14/7 という計算を行う場合、5、10、15、、25、30、35が5の倍数、さらに、7、14、21、28、35が7の倍数に含まれています。